Сумма внутренних углов выпуклого n-угольника вычисляется по формуле: 180° × (n - 2), где n - количество сторон многоугольника.
Содержание
Основная теорема о сумме углов многоугольника
Примеры для различных многоугольников
| Многоугольник | Количество сторон (n) | Сумма углов |
| Треугольник | 3 | 180° × (3-2) = 180° |
| Четырехугольник | 4 | 180° × (4-2) = 360° |
| Пятиугольник | 5 | 180° × (5-2) = 540° |
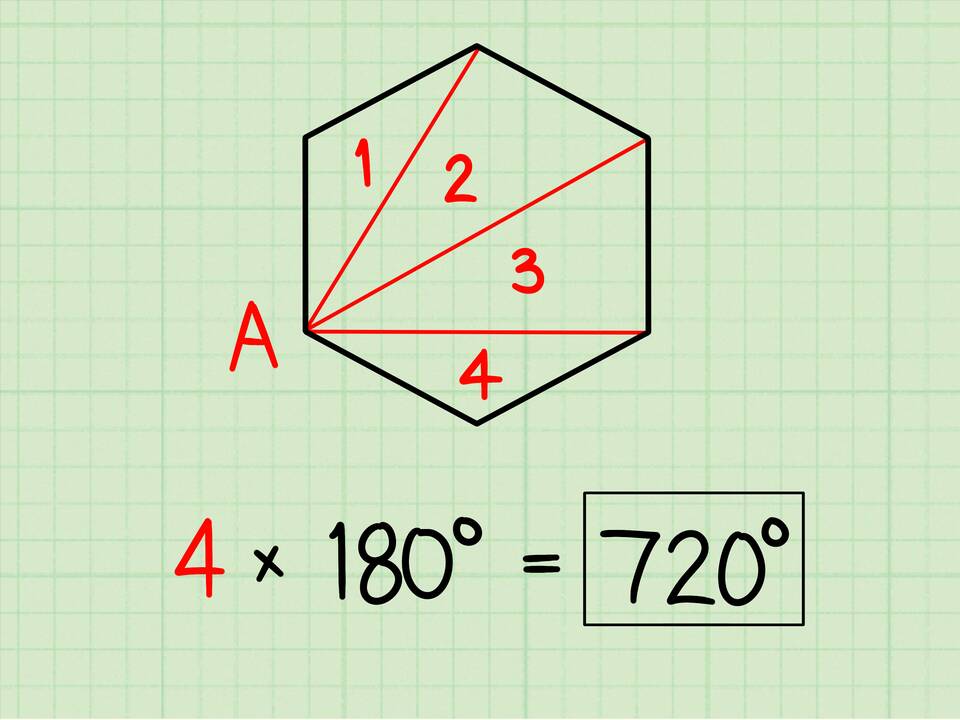
| Шестиугольник | 6 | 180° × (6-2) = 720° |
Доказательство формулы
Метод разбиения на треугольники
- Выбираем одну вершину многоугольника
- Проводим диагонали из этой вершины ко всем несмежным вершинам
- Многоугольник разбивается на (n-2) треугольников
- Сумма углов каждого треугольника равна 180°
- Общая сумма: 180° × (n-2)
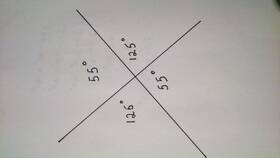
Сумма внешних углов многоугольника
- Для любого выпуклого многоугольника сумма внешних углов равна 360°
- Это правило работает независимо от количества сторон
- Каждый внешний угол дополняет внутренний до 180°
Сравнение внутренних и внешних углов
| Тип углов | Сумма для n-угольника |
| Внутренние | 180° × (n-2) |
| Внешние | 360° (для любого n) |
Практическое применение
Где используются эти знания
- В архитектуре при проектировании зданий
- В компьютерной графике при моделировании объектов
- В геодезии при измерении участков земли
- В школьном курсе геометрии
Пример расчета для восьмиугольника
- Количество сторон n = 8
- Применяем формулу: 180° × (8-2)
- Получаем: 180° × 6 = 1080°
- Средняя величина внутреннего угла: 1080° / 8 = 135°